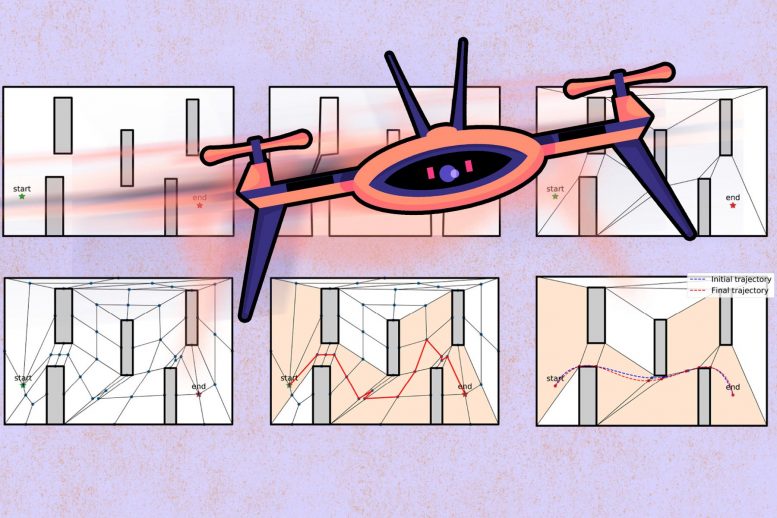
Aerospace engineers at MIT have devised an algorithm that helps drones find the fastest route around obstacles, without crashing. Credit: MIT News, with background figure courtesy of the researchers
New algorithm could enable fast, nimble drones for time-critical operations such as search and rescue.
If you follow autonomous drone racing, you likely remember the crashes as much as the wins. In drone racing, teams compete to see which vehicle is better trained to fly fastest through an obstacle course. But the faster drones fly, the more unstable they become, and at high speeds their aerodynamics can be too complicated to predict. Crashes, therefore, are a common and often spectacular occurrence.
But if they can be pushed to be faster and more nimble, drones could be put to use in time-critical operations beyond the race course, for instance to search for survivors in a natural disaster.
Now, aerospace engineers at 
A quadcopter flies a racing course through several gates in order to find the fastest feasible trajectory. Credit: Courtesy of the researchers
The researchers found that a drone trained with their algorithm flew through a simple obstacle course up to 20 percent faster than a drone trained on conventional planning algorithms. Interestingly, the new algorithm didn’t always keep a drone ahead of its competitor throughout the course. In some cases, it chose to slow a drone down to handle a tricky curve, or save its energy in order to speed up and ultimately overtake its rival.
“At high speeds, there are intricate aerodynamics that are hard to simulate, so we use experiments in the real world to fill in those black holes to find, for instance, that it might be better to slow down first to be faster later,” says Ezra Tal, a graduate student in MIT’s Department of Aeronautics and Astronautics. “It’s this holistic approach we use to see how we can make a trajectory overall as fast as possible.”
“These kinds of algorithms are a very valuable step toward enabling future drones that can navigate complex environments very fast,” adds Sertac Karaman, associate professor of aeronautics and astronautics and director of the Laboratory for Information and Decision Systems at MIT. “We are really hoping to push the limits in a way that they can travel as fast as their physical limits will allow.”
Tal, Karaman, and MIT graduate student Gilhyun Ryou have published their results in the International Journal of Robotics Research.
Fast effects
Training drones to fly around obstacles is relatively straightforward if they are meant to fly slowly. That’s because aerodynamics such as drag don’t generally come into play at low speeds, and they can be left out of any modeling of a drone’s behavior. But at high speeds, such effects are far more pronounced, and how the vehicles will handle is much harder to predict.
“When you’re flying fast, it’s hard to estimate where you are,” Ryou says. “There could be delays in sending a signal to a motor, or a sudden voltage drop which could cause other dynamics problems. These effects can’t be modeled with traditional planning approaches.”
To get an understanding for how high-speed aerodynamics affect drones in flight, researchers have to run many experiments in the lab, setting drones at various speeds and trajectories to see which fly fast without crashing — an expensive, and often crash-inducing training process.
Instead, the MIT team developed a high-speed flight-planning algorithm that combines simulations and experiments, in a way that minimizes the number of experiments required to identify fast and safe flight paths.
The researchers started with a physics-based flight planning model, which they developed to first simulate how a drone is likely to behave while flying through a virtual obstacle course. They simulated thousands of racing scenarios, each with a different flight path and speed pattern. They then charted whether each scenario was feasible (safe), or infeasible (resulting in a crash). From this chart, they could quickly zero in on a handful of the most promising scenarios, or racing trajectories, to try out in the lab.
“We can do this low-fidelity simulation cheaply and quickly, to see interesting trajectories that could be both fast and feasible. Then we fly these trajectories in experiments to see which are actually feasible in the real world,” Tal says. “Ultimately we converge to the optimal trajectory that gives us the lowest feasible time.”
Going slow to go fast
To demonstrate their new approach, the researchers simulated a drone flying through a simple course with five large, square-shaped obstacles arranged in a staggered configuration. They set up this same configuration in a physical training space, and programmed a drone to fly through the course at speeds and trajectories that they previously picked out from their simulations. They also ran the same course with a drone trained on a more conventional algorithm that does not incorporate experiments into its planning.
Overall, the drone trained on the new algorithm “won” every race, completing the course in a shorter time than the conventionally trained drone. In some scenarios, the winning drone finished the course 20 percent faster than its competitor, even though it took a trajectory with a slower start, for instance taking a bit more time to bank around a turn. This kind of subtle adjustment was not taken by the conventionally trained drone, likely because its trajectories, based solely on simulations, could not entirely account for aerodynamic effects that the team’s experiments revealed in the real world.
The researchers plan to fly more experiments, at faster speeds, and through more complex environments, to further improve their algorithm. They also may incorporate flight data from human pilots who race drones remotely, and whose decisions and maneuvers might help zero in on even faster yet still feasible flight plans.
“If a human pilot is slowing down or picking up speed, that could inform what our algorithm does,” Tal says. “We can also use the trajectory of the human pilot as a starting point, and improve from that, to see, what is something humans don’t do, that our algorithm can figure out, to fly faster. Those are some future ideas we’re thinking about.”
Reference: “Multi-fidelity black-box optimization for time-optimal quadrotor maneuvers” by Gilhyun Ryou, Ezra Tal and Sertac Karaman, 29 July 2021, International Journal of Robotics Research.DOI: 10.1177/02783649211033317
This research was supported, in part, by the U.S. Office of Naval Research.